Страница 4. Связь треугольник Паскаля с арифметическими прогрессиями высших порядков

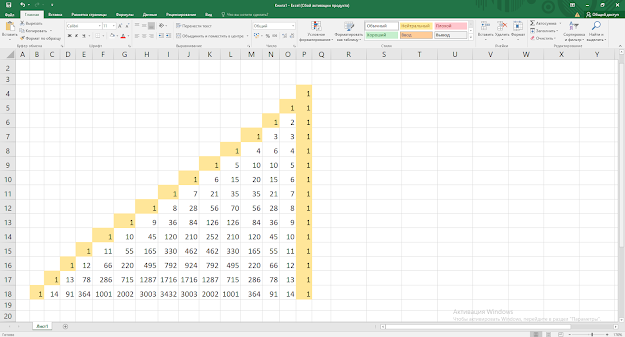
Треугольник Паскаля - это бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

Если хочешь подробнее узнать про треугольник Паскаля, то советую посмотреть данный видеоролик:

Его можно охарактеризовать как бесконечную таблицу. В данной таблице используются биномиальные коэффициенты. А сама таблица представлена в виде треугольника. Чтобы произвести расчет, можно использовать калькулятор, где указывается только количество строк. При самостоятельном расчете потребуется время и знание формул.

Как уже говорилось, данный треугольник представляет собой таблицу, начинается которая с нулевой строки. Вершина таблицы и боковые стороны каждой строки имеют единицы. Остальные числа (в середине) равны сумме 2-ух чисел, которые находятся в предыдущей строке (над ними).

В данном случае используются натуральные степени бинома: х+у
Для нулевой строки: (x + y)° =
Для первой: (x + y)¹ =
Для второй: (x + y)² =
И так далее.
Если разложить в сумму одночленов, получим для нулевой: 1
Для первой: 1x + 1y
Для второй: 1x² + 2xy + 1y²
Треугольника Паскаля, для расчетов используется формула: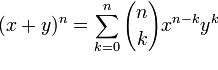

Треугольник Паскаля прост, но в то же время таит в себе неисчерпаемые сокровища и связывает воедино различные разделы математики, не имеющие на первый взгляд ничего общего. Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа и их обобщения на случай пространств всех размерностей. Суммы чисел, стоящих вдоль восходящих диагоналей, образуют хорошо известную последовательность чисел Фибоначчи.

Докажем, что две строки из треугольника - арифметические прогрессии 8-го и 9-го порядков.

Чтобы нагляднее рассмотреть треугольник, можете как и я, построить его в приложении Excel.

В верхней строчке треугольника располагается одинокая единица. В остальных строках каждое число является суммой двух своих соседей этажом выше — слева и справа. Если какой-то из соседей отсутствует, он считается равным нулю. Треугольник бесконечно простирается вниз; мой пример включает 14 строк.

Исследуя связь треугольника Паскаля с арифметическими прогрессиями высших порядков, я выделила 8-ой и 9-ый порядки в моем, ранее построенном, треугольнике:

Исходя из этого делаю вывод, что треугольник Паскаля имеет связь с арифметическими прогрессиями высших порядков. 

Главная

←Назад

Далее→